Advanced P2P Guide

ABSTRACT

This paper aims to develop a risk-return profiling approach for Peer-to-Peer platforms. We develop a top-down approach to risk budget different subcomponents of Peer-to-Peer platforms. As the risk distributions of the Peer-to-Peer platforms are typically skewed with extreme risks, we use coherent measures of risk and shortfall measures that can be aggregated consistently across different risks. This approach can be used by decision makers to choose optimal portfolio combinations of Peer-to-Peer loan portfolios and analyze the risk profiles of platforms. We apply the method to Lending Club data and we extract the loss distributions for the different risk buckets of loan portfolios, which enables us to evaluate expected returns as well as the expected losses and the expected shortfalls. Our method can be used as a risk management and portfolio optimization tool for any decision maker who can fix his confidence level that implies a certain aggregate risk budget.

KEYWORDS: Risk Management, FinTech, Portfolio selection, Coherent aggregation
JEL CLASSIFICATION: G11, D81, C11

INTRODUCTION

Recent financial innovations and the development of digital technologies have considerably changed the landscape and the business models of the finance industry. Hence, the development of Fintech, defined by the Financial Stability Board (2017) as “technologically enabled financial innovation that could result in new business models, applications, processes or products with an associated material effect on financial markets and institutions and the provision of financial services”, might have major impacts on the sector of credit institutions, a process analyzed by Stulz (2019). This has led, however, to concerns about financial stability if this sector grows. The sector of fintech credit poses specific regulatory and risk management challenges (CGFS-FSB (2017)). Although, there is no internationally agreed definition, it broadly includes all credit activity implemented through electronic platforms not operated by commercial banks. It encompasses activity implemented through borrower and lender matching platforms. In different jurisdictions those platforms might take different denominations like “peer-to-peer (P2P) lenders”, “loan-based crowd-funders” or “marketplace lenders” and be regulated in different ways. Those platforms also differ in the way they use their own balance sheets, provide guarantees, work with loan originators and have institutional investors. Those platforms that belong to the so-called alternative credit market are also increasingly becoming a new asset class for some investors. In the US, for instance, approximately 60% of P2P funding is financed by institutional investors and the activity is now referred to as “marketplace lending”. Recent trends include institutional investors funding bulks of credits with eventually some securitization process involved (US Department of the Treasury (2018)). The different types of platforms with their different business models, however, are likely to hide different types of risks. Whereas financial risks are typically measured with risk measures adapted to measure market, credit and liquidity risk, the different business model risks, have to be analyzed through agency mechanisms stemming from asymmetries of information between different parties. Ideally, the risk inherent in such a platform should be quantified and aggregated with the investment risk implicit in the structure’s portfolio. The third type of risk stems from operational risk. As the degree of digitalization of the platforms is much higher than for other institutions the main operational risk is given by cyber risks, a serious threat for such structures. To assess the aggregate risk of the different types of platforms, some kind of aggregate risk measure needs to be developed. The problem, however, is that the risk distributions of the different components differ. The task is thus to aggregate risks for different types of risk distributions. Such a process supposes that risk measures are coherent (Artzner et al. (1999)). This is a problem of coherent aggregation of risk measures analyzed by Kalkbrener, M. (2005), Dorfleitner, G. and Buch, A. (2008), Fischer, T. (2003). The typical risk measure that respects all coherency principles and is adapted to the different risk distributions is expected shortfall (Acerbi, C. and Tasche, D. (2002)).

The modelling of credit risks also poses particular challenges. For an overview of consumer credit risks (Livshits (2015)). Recently, the operations research (OR) literature has become interested in the modelling of P2P platforms’ loss distributions. Most studies focus on the two largest P2P platforms in the US, namely Prosper and Lending Club. The credit supply process implicit in P2P lending, however, differs from standard retail banking. Even though P2P platforms screen potential borrowers against their own criteria, once the loan is listed on the platform the investors bear the risks. This is in contrast with bank lending where banks bear the risk and the get the return. It is important to highlight that P2P platforms have different business models that might also entail different kinds of risks. The business model of the platform is thus also of foremost importance.

The P2P platforms have recently attracted, not only retail investors, but also institutional investors. For instance, Balyuk and Davydenko (2018) indicate that for the Prosper platform, 90% of loans were provided through institutional channels. They also suggest that active strategies may yield more than passive institutional strategies. Thus, a framework to analyze the risk-return profiles of P2P portfolios and/or platforms is of foremost interest.

LITERATURE REVIEW OF TOPIC 1: (Operational research approach)

The first focusses on P2P loan scoring methods. Recent approaches are developed in Kim et al. (2019), Verbraken et al. (2014), Serrano-Cinca and Gutierrez-Nieto (2016), Guo et al. (2016). The finance perspective also focuses on how investors adapt the platforms’ operations, business models and available information (Miller (2015), Balyuk and Davydenko (2018), Jagtiani and Lemieux (2017), Vallee and Zheng (2019)). Apart from factors linked to creditworthiness, the finance literature also focuses on softer information. The softer information, however, is more costly to verify than harder information (Liberty and Peterson (2019)).

Recently, Fitzpatrick and Mues (2021) investigated the combination of different approaches. Their study is based on Lending Club data and they analyze loan level predictors based on a combination of loans, borrowers, credit risk and text derived characteristics. As the marketplace lending platforms are a new type of emerging institutions, not much is known about potential risk management solutions. Claessens et al. (2018) also argue that recent experiences lead to fundamental challenges for users, regulators and investors.

What is the degree of risk transparency and disclosure of the platforms and do investors and borrowers really understand them? Are the interest rates and fees of the platform in line with the potential risk and expectations? What is the underlying degree of complexity and what kinds of risks does it hide? Are the operational risk management, notably data- and cyber-security systems adequate?

The aim of this paper is to provide a solution to those challenges by analyzing those platforms’ ecosystems and develop an integrated risk management approach. The objective is to measure the risk for each component so to be able to diagnose the specific risks of each component for a respective platform as well the aggregate risk, namely total aggregate risk of investment, knowing that the risk might be allocated to different substructures. Such an aggregation procedure, however, is not straightforward and depends on the risk measures that are used in the process. We use coherent risk and shortfall measures that are consistent with a coherent aggregation process. This means that we can set risk budget targets that can be consistently aggregated making sure that the total risk is in line with the target risk. In section 1, we describe the process to measure and aggregate risk in a coherent way. Section 2 presents the portfolio optimization approach to determine the risk-return allocation in the FinTech structure. In section 3, we use a factor model approach to model the loss distribution of underlying portfolios. Finally, section 4 presents the empirical implementation of the method.

Financial Risk and Coherent Aggregation

Capital allocation is obviously a major topic for financial institutions in order to determine the global risk buffer and to benchmark different business units to ensure that value added is in line with the risks incurred. One of the major challenges, however, rests with the aggregation and decomposition of risk capital across different business lines. The BIS defines economic capital as “the methods or practices that allow financial institutions to attribute capital to cover economic effects of risk-taking activities”. The ability of economic capital models to adequately reflect business-line operating practices and therefore provide appropriate incentives to business units is also an issue. Finally, our major challenge, here, is the development of any simple risk measure to capture adequately all the complex aspects of Fintech platform risks.

Economic capital is the amount of capital a financial institution needs to absorb unexpected losses over a certain time horizon at a given confidence level. Expected losses are typically accounted for in the pricing of a financial institution’s products and loan loss provisions. It is thus unexpected losses that require economic capital. Issues with the implementation of economic capital allocation arise at different levels. Credit portfolio management aims at improving the riskadjusted return profiles of credit portfolios via credit risk transfer transactions and control of the loan approval process. Loan’s marginal contributions to the portfolio’s economic capital and riskadjusted performance are the major criteria. The economic capital can then be used to price the credit products. Risk-adjusted performance is measured with RAROC. In order for economic capital to be totally integrated in the internal decision process, economic capital needs to be integrated into the objective functions of the decision makers.

Typically, financial institutions’ relative performance is measured with risk-adjusted performance measures based on economic capital. The most common risk-adjusted performance measures are RAROC (Risk-adjusted Return on Capital). Whereas RAROC measures performance compared to risk. In order to evaluate RAROC, a hurdle rate, which reflects the financial intitutions’s cost of capital, as well as a confidence level to evaluate economic capital have to be set. Economic capital plays an important role in the hypothetical capital allocation for the budgeting process. This process is an important component of the strategic planning and the target setting. Strategic planning involves setting the risk appetite, whereas target setting involves, for instance, deciding on an external rating. The economic capital allocation process may depend on the governance structure of the financial institution, in our case the business model of Fintech credit platform. In a standard financial institution, after economic capital is allocated, the business unit’s managers are supposed to manage risk so that it does not exceed economic capital. Depending on how centralized the management of the bank is, internal allocation of capital at the business unit is delegated to the business managers. In the case of Fintech credit platforms, the process might be diluted as there is no centralized evaluation of risks and economic capital with risk limits.

The most widely used risk measures are Value at Risk (VaR) and Expected Shortfall (ES). VaR is the most intuitive measure and it is the easiest to communicate. However, as it is not subadditive whenever risks are not elliptically distributed, it can cause problems in terms of internal capital allocation and limit settings. ES is less easily interpreted, but is generally sub-additive and can be used to set risk limits consistent with the aggregate target risk. In order for those risk measures to be calculated, a confidence interval has to be fixed. The latter is often function of an external rating target and the confidence interval is interpreted as the economic capital necessary to prevent an erosion of the capital buffer. The relationship between external ratings and PD’s is not necessarily very stable and the targeting of an external rating might be difficult to realize. Other considerations such as risk allocation to different business lines to measure profitability might call for lower confidence levels. Incidentally, the confidence interval might make portfolios look relatively better or worse depending on the distribution of extreme risks.

As already alluded to, a main issue rests with the aggregation and decomposition of risk measures. Decomposition refers to the fact that within a portfolio, risk needs to be decomposed to analyse the risk inherent to each position. Decomposition is important to determine capital allocation, limit setting, pricing of products and risk-adjusted performance measurement. Aggregation properties are important to determine the financial institutions’s overall economic capital from market, credit, operational and other risks.

In order to aggregate risks, financial institutions have to categorize the sources of risk into risk units. They are typically categorized along two dimensions: the economic nature of the risks, namely credit, market and operational risks, and the organizational structure of the financial institution. Even though classification along organizational lines such as business lines is straightforward, the disentangling of market, credit and operational risk can be quite difficult. In the case of fintech trading platforms, given the eventual complexity of the Business Models, the risk inherent in the organizational structure might be more difficult to evaluate, a topic further discussed in the next section.

The main difficulty with aggregation however rests with the elaboration of the unit of risk account, also known as common risk currency. Typically, units of risk account depend on three characteristics. First, the risk metric should be in line with the risk metrics used to measure individual risk components and, here, sub-additivity of the risk metric is a major issue. Second, when distributions of risks do not share the same distributional assumptions, the specification of confidence levels is likely to impact the risk aggregation process. Finally, the determination of the time horizon for the aggregation is not straightforward, as the different risk components (market and credit notably) are measured in different units of time. Typically, the time horizon is fixed at one year.

Different aggregation methodologies are used by financial institutions. The easiest way to aggregate the risks is to use the sum of the risks. This is a conservative measure of economic capital as it is not taking into account potential diversification effects and might lead to lower performance on economic capital. Some institutions thus implement a slightly more advanced approach by fixing a diversification percentage coefficient. The approach presumes that the adding of risks leads to a predetermined diversification effect, the latter being difficult to specify in practice. Aggregation can also be implemented on the basis of a variance-covariance matrix, even though this approach bears on the assumption that risks are multivariate normally distributed. In order to circumvent this problem, the most consistent approach is to model common risk drivers across all portfolios and aggregate the risks with a copula, which allows for risk aggregation with marginal risk components that are not normally distributed.

Our approach, here, is to evaluate the risk capital that is implicit in the activities of the FinTech Credit platforms activities. We thus have to aggregate the different risk capital viewed as some kind of risk budget for different structures involved in the FinTech Credit Business Model. The aggregate risk capital can then be compared to the aggregate effective capital held by the FinTech credit Business Model, to determine the implicit probability of default, which can be used to map it on a potential rating. In order to analyse that question more formally we need to focus more in detail on the properties of the risk measures used.

(Artzner et al., 1999) derived the axioms that a well-behaved risk measure should respect. A socalled coherent risk measure 𝜌(𝑋) is a real valued function defined on the space of real-valued random variables, which satisfies the following axioms:

1) Translation invariance  ∀𝑐𝜖R, 𝜌(𝑋 + 𝑐) = 𝜌(𝑋) − 𝑐

2) Sub-additivity  ∀𝑋, 𝑌, 𝜌(𝑋 + 𝑌) ≤ 𝜌(𝑋) + 𝜌(𝑌)

3) Positive homogeneity ∀𝜆 ≥ 0, 𝜌(𝜆𝑋) = 𝜆𝜌(𝑋)

4) Positivity 𝑋 ≥ 0, 𝜌(𝑋) ≤ 0

All those axioms have a specific interpretation. Translation invariance, also called cash-invariance, implies that the risk can be interpreted in terms of capital requirements, a property we need to compare risk capital to the effective capital held by the FinTech credit Business Model. If an investor puts the amount 𝜌(𝑋) of cash in the structure, the structure becomes riskless under a certain probability. It thus indicates the amount of risk capital the structure should have, given the risk measure used 𝜌. Positivity, of course, just implies that a higher payoff profile has less risk. A measure that satisfies both axioms is called a monetary measure of risk (Föllmer & Scheid, 2008). Positive homogeneity means that an increase in all the portfolio positions by λ also leads to a linear increase in the risk involved. This axiom has actually been questioned on the grounds of liquidity risk. In our case, it implies that the increase in volume of the FinTech structure does not increase the risk more than proportionally. Finally, sub-additivity which is probably the most important axiom implies that the risks of a portfolio are less than the sum of individual risks. A well-behaved risk measure should thus model diversification effects. This property enables us to aggregate the different risk capital values across the whole FinTech structure in a consistent way.

This last property can also be used from an active management perspective to decentralize the task of managing the risks arising from a collection of different components of the FinTech Credit Structure. Separate risk limits can potentially be set for the different components making sure that the risk of the aggregate FinTech Credit Platform is bounded by the sum of individual risk limits, which of course would be conditioned by the default probability. That default probability can then be linked to certain target rating. In many risk management problems, the following VAR measure is used.

As alluded to earlier, VaR is not sub-additive when tail risk is high which is quite likely the case for some risks in the FinTech credit structure.

Expected shortfall given by

ES_λ=1/λ*∫₀^λVaR_α(X)dα

is a coherent risk measure and can be used as an effective risk measure to set decentralized risk limits. ES also has other interesting properties in terms of manager control and robustness. As highlighted by (Basak & Shapiro, 2001), risk limits in terms of VAR may lead to portfolio concentrations and increases of extreme risks. ES measures can also be deduced from robust decision making in the face of uncertainty (Föllmer & Schied, 2004). The development of coherent risk measures has also led to research on coherent capital allocation which is of particular interest here.

Coherent capital allocation has been a research topic since the seminal work of Artzner et al. (1999) and is important to consistently allocate risk capital to the different subunits of the FinTech structure. The first major contribution to the issue of coherent economic capital allocation was provided by Denault (2001). He analyses how adding different business units or sub-portfolios leads to diversification effects, thus the sum of the risks of the subcomponents is larger than the risk of the sum of the subcomponents. We want to analyse the total risk capital of a FinTech structure taking into account the diversification effects and dividing the risk capital among the sub- units.

Kalkbrener (2005) develops an axiomatic approach and shows that sub-additivity and positive homogeneity of risk measures is of foremost importance. The suggested axiomatization presumes that the risk capital allocated to a sub-unit i depends exclusively on the risk of sub-unit i and the risk of the whole FinTech structure, not on the decomposition of the other sub-units. The axiomatization of Kalkbrener (2005) is based on the assumption that capital allocated to sub-unit 𝑆𝑈_i only depends on 𝑆𝑈_i and the aggregate FinTech Structure S, but not on the decomposition of the rest of the portfolio S−𝑆𝑈_i = ∑_i≠j 𝑆𝑈_i. The capital allocation rule is thus represented by a function Φ(𝑆𝑈_i,𝑆). If we consider an aggregate risk measure 𝜌(𝑆), fixed by a decision maker for instance, then Φ is a capital allocation with respect to 𝜌(𝑆) whenever Φ(𝑆, 𝑆) = 𝜌(𝑆), hence when the capital allocated to the aggregate portfolio equals the risk capital of the aggregate FinTech structure.

Three axioms are important for coherent capital allocations across the FinTech structure. First, linear aggregation makes sure that the sum of the risk capital of the sub-units equals the risk capital of the aggregate FinTech structure. Second, as mentioned earlier there are some diversification effects. Third, continuity ensures that small sub-unit adjustments have a limited impact of the risk capital of the aggregate structure. Those axioms uniquely characterize capital allocations. Also, for a given risk measure 𝜌 there exists a capital allocation Φ_𝜌 that satisfies the linear aggregation and diversification axioms if and only if 𝜌 is sub-additive and positively homogeneous, that is 𝜌 satisfies:

𝜌(𝑆𝑈_i + 𝑆𝑈_j) ≤ 𝜌(𝑆𝑈_i) + 𝜌(𝑆𝑈_j)

𝜌(𝜆𝑆𝑈_i) = 𝜆𝜌(𝑆𝑈_i), ∀𝜆 ≥ 0

The existence of directional derivatives of 𝜌 at the aggregate level S is a necessary and sufficient condition for Φ_𝜌 to be continuous at S.

The following if conditions can be used to set up the coherent risk capital process across the Fintech credit structure.

1. If there exists a linear, diversifying capital allocation Φ_𝜌 with respect to 𝜌, then 𝜌 is positively homogeneous and sub-additive.
2. If 𝜌 is positively homogeneous and sub-additive then Φ_𝜌 is a linear, diversifying capital allocation with respect to 𝜌.

We suggest now to integrate shortfall measures in an optimizing framework. This is an approach pioneered by Bertsimas et al. (2004). Instead of maximizing the return for a given risk, the return is mapped on potential risk factors and the distance between the return and the expected shortfall is then minimized. The allocation should be optimal given an aggregate shortfall measure that could be determined by an investor or the decision maker of a FinTech credit structure. The aggregate measure can then be used to evaluate the aggregate capital of the FinTech Structure to the aggregate risk capital for a given targeted rating. We first develop the general mathematical framework before elaborating on the application to the specific FinTech Structure.

General Portfolio optimization with shortfall measures

Let’s now consider a vector of expected returns 𝐸(𝑅) that are potentially linked to the risk profile of a subset of borrowers, with mean

𝐸(𝑅) = 𝜇

and a vector of portfolio weights ω. As we will concentrate on risk measurement and rating of a FinTech structure, the mean return will be fixed at a target return rate for a portfolio of borrowers.

𝐸[𝑅^T𝜔] = 𝑅_p

Depending on the respective DM, however, this value could be fixed as expected loss if they are provisioned and we have a risk management perspective.

As mentioned earlier, we could now minimize over ω the (1-α) confidence level

𝑉𝑎𝑅_𝛼(𝜔): = 𝜇^T𝜔 − 𝑞𝛼(𝑅^T𝜔), ∀𝛼 ∈ (0,1)

where 𝑞_𝛼(𝑅^T𝜔) is the α-quantile of the distribution of the portfolio return 𝑅^T𝜔. The 𝑞_𝛼(𝑅^T𝜔) would then be fixed to be consistent with a certain probability of default linked to the parameter α. A natural approach of portfolio optimization would thus consist in minimizing 𝑉𝑎𝑅_𝛼 as a function of portfolio weights. From an operational perspective the FinTech structure should thus be such that it minimizes the 𝑉𝑎𝑅_𝛼 for a given return of the underlying return on the sub-portfolios of borrowers.

Issues with sub-additivity rather lead us to use shortfall to impose limits on deviations of losses with respect to the expected return. We thus suggest to minimize the shortfall at the risk level α and as we reason in terms of losses:

𝑠_𝛼(𝜔):=𝜇^T 𝜔 − 𝐸 [𝐿^T 𝜔 | 𝐿^T 𝜔 ≥ 𝑞_𝛼 (𝐿^T 𝜔) ] , ∀𝛼 ∈ (0,1)

s_𝛼 (𝜔) basically, measures the expected losses below the expected return that might occur whenever the portfolio drops below the α-quantile. It measures how much is lost on average when things go really bad. Given those results we are led to focus on shortfall minimization. In order to analyze the risk capital of the FinTech structure we need a risk budgeting process.

The risk measure originally introduced by (Artzner et al, 1999) was not expected shortfall but Tail Conditional Expectation

𝑇𝐶𝐸_𝛼(𝜔) = −𝐸[𝐿^T 𝜔|𝐿^T 𝜔 ≥ 𝑞_𝛼(𝐿^T 𝜔)]

Which is a coherent risk measure.

As shortfall is to be used in portfolio optimization it integrates the expected return and shortfall can be expressed as the following way:

𝑠_𝛼(𝜔) = 𝜇^T𝜔 + 𝑇𝐶𝐸_𝛼

Due to this mean-adjustment, expected shortfall violates translation invariance and positivity. Shortfall has other useful mathematical properties. Most notably, an important issue for portfolio optimization is that it is convex in the portfolio weightsw which is not necessarily the case with VaR.

Moreover:

1. 𝑠_𝛼(𝜔) ≥ 0 ∀𝜔 𝑎𝑛𝑑 𝛼 ∈ (0,1). 𝑠_𝛼(𝜔) equals 0 for some ω and α if and only 𝐿^T 𝜔 is constant with probability 1.
2. 𝑠_𝛼(𝜔) is positively homogeneous: 𝑠_α(𝜆𝜔) = 𝜆𝑠_α(𝜔),∀𝜆 ≥ 0
3. In case the density of losses is continuous, we get 𝛻_𝜔𝑠_α (𝜔) = 𝜇 − 𝐸 [ 𝐿 | 𝐿^T𝜔 ≥ 𝑞_α  (𝐿^T 𝜔)]

Those properties are useful to create a risk budgeting process that can be used to analyse the risks of the FinTech structure but also guide an operational risk management process.

If we can simulate the loss distribution of a reference portfolio of loans, shortfall can be estimated quite easily. Consider a simulated sample of N losses of a portfolio of loans ω. The losses can then be ranked from the lowest indexed by 1 to the highest indexed by N. 𝑙_i(𝜔) and the losses can be sorted in increasing order:

𝑙₁(𝜔) ≤ 𝑙₂(𝜔) ≤. . . ≤ 𝑙_N(𝜔)

Consider 𝐾 = [𝛼𝑁], the number of losses above a certain level, the non-parametric estimator of 𝑠_α(𝜔) can be represented thus: 

s_α(w)=ω^Tμ -1/K *∑_j=1^Kl_(j)(ω)

From an operational risk management viewpoint, the following mean-shortfall optimization can be solved to determine the optimal allocation of risk within a FinTech structure.

Minimize 𝑠_α(𝜔)

subject to  𝜔^T𝜇 = 𝑟_p 𝑎𝑛𝑑 𝑒^T𝜔=1

where e is a column vector of ones.

Bertsimas et al. (2004) show that the minimum α-shortfall frontier is convex. In presence of a riskless asset the minimum shortfall is defined from:

Minimize 𝑠_α(𝜔)

Subject to 𝜔^T𝜇 + (1 − 𝑒^T𝜔)𝑟_f =𝑟_p

(Tasche, 2000) has shown that the minimum shortfall frontier in the (𝑟_p,  𝑠_α (𝜔)) space, with 𝑟_p ≥ r_f , is a ray starting from the point (r_f , 0). and passing through the particular point (r^*_p, s^*_α(𝜔))

with 𝑟^∗_p ≥ 𝑟_f .

The optimal solution satisfies

𝜇_j − 𝑟_f = 𝛽_j,α (𝜔_α) (𝑟_p −𝑟_f), 𝑗 = 1 ,..., 𝑛

With

β_j,α(ω)=1/s_α(ω)* ∂/∂ω_j s_α(ω) = (μ_j-E(L_j|ω^TL≥q_α(L^Tω))/(ω^Tμ - E(ω^TL|ω^TL≥q_α(L^Tω)))

𝛽_j,αis called the shortfall beta and can be used to measure the relative change in shortfall when varying and allocating loans across the FinTech structure. Note that the following characteristic that will be useful for the risk budgeting process holds.

∑_j=1ⁿω_jβ_j,α(ω)=1

This is a very useful property as it gives a decomposition of a portfolio shortfall into individual contributions of loans or substructures of the FinTech structure. As mentioned earlier it can be used to measure the risk capital of any financial structure but also as a tool where the management can fix a shortfall target and given Euler’s Theorem applies to the measure, to deduce:

s_α(ω) = ∑_j=1ⁿω_j*(∂/∂ω_j)s_α(ω)

More exactly:

μ(ω)=-E(ω^TL|ω^TL≥q_α(L^Tω)) = ∑_j=1ⁿω_j* [μ_j-E(ω^TL|ω^TL≥q_α(L^Tω))]

Different approaches can now be used to evaluate or simulate the loss distributions.

The factor model approach

This approach underlies portfolio models based on a structural approach where default occurs when some value of a latent process falls below a limit. The main advantage is that it reduces the dimensionality of the dependence problem for large portfolios. A latent factor drives the default process. When the value of the latent factor is below a threshold value, the borrower defaults. The latent factors are assumed to depend on a common factor as well as an idiosyncratic term specific to each borrower and uncorrelated to the common factor. Within the standard approach, the factors are assumed normally distributed. This is the so-called Gaussian Copula model. In general, the factors are assumed to be normally distributed and are scaled to have unit variance and zero expectation. In case, of heavy tail dependence of the risks, however, the model can be adapted to take into account stronger tail distributions of the factors. This then leads to the so-called student t-copula. As the market standard for pricing credit risk is the Vasicek (2002) asymptotic single factor model, we will consider the model in more detail here and eventually adapt it later to a more complex environment.

It is assumed that the dynamic of an obligor n’s wealth is given by a continuous-time geometric Brownian motion:

dS_n,t/S_n,t=μ_ndt+σ_ndε_n,t

where 𝜇u is the expected return, 𝜎u the instantaneous volatility and 𝜀_n,t^t the standard Brownian motion.

It is now assumed that default occurs when the Brownian motion falls below a limit L. The probability of default, given the value of the Brownian motion at time t, is given by:

p_n,t,T=P[S_n,t<L|S_n,t]

By applying Itô’s lemma we can derive the value of the Brownian motion at time T as a function of its current value:

S_n,T=S_n,texp(μ_n-σ_n²/2)*(T-t)

where 𝑑𝜀_n,t,T is given by:

dε_n,t,T=(ε_n,T-ε_n,t)/sqrt(T-t)

Default then amounts to 𝑑𝜀_n,t,T < 𝐾_n,t,T where

K_n,t,T=(lnL_n-lnS_n,t-(μ_n-σ_n²/2)*(T-t))/(σ_n*sqrt(T-t))

The calculations are similar to the ones implemented to derive the B&S formula and the probability of default can hence be expressed by : p_n,t,T = Φ(K_n,t,T )where Φ is the distribution function of standard normal random variable. By simulating different paths of the Brownian motion, we can determine the default probability for different borrowers n. If we can find similar types of reference borrowers, the limit K can also be calibrated by inverting the phi function 𝜙^-1(𝑝_n) = 𝐾. There might, however, exist some default correlation that we have to take into account in the shock process. This is typically done with a factor model.

In consistency with the model above, consider a portfolio of N obligors where each obligor defaults as soon as the relevant latent factor 𝑆_n,t drops below L. In order to derive a closed form for the portfolio default rate, namely the fraction of defaulted credits in the portfolio at time t, Vasicek (2002) made a few assumptions. The portfolio default rate will be determined by the individual default rates as well as the default correlations. Those correlations will affect the random variables 𝑑𝜀_n,t and create common effects accross borrowers. Vasicek assumes that the correlation coefficient between any pair of random variables is the same for any two obligors, hence:

corr(dε_n,t,dε_m,t)=ρ_n,m,t=ρ_t∀n≠m

A common correlation coefficient then partly drives all the obligor’s latent factor processes. The idea is that there exists a random systemic factor that impacts the latent factor of all the obligors. The random variables triggering default can now be written:

dε_n,t=sqrt(ρ)M_t+sqrt(1-ρ)z_n,t

Default is determined by two factors: M_t which is a common or systematic factor and 𝑧_n,t which is an idiosyncratic factor. M_t generates the default dependency as it affects all obligors in the same way. This model is equivalent to the Gaussian copula. The default probability at time t can now be evaluated by conditioning on the common factor M_t.

p_n(M_t)=P[dε_n,t<K_n,t|M_t]=P[z_n,t<(K_n,t-sqrt(ρ_t)M_t)/sqrt(1-ρ_t)|M_t]=φ((K_n,t-sqrt(ρ_t))/sqrt(1-ρ_t))

Conditionally on M_t the default probabilities are independent. It is assumed that we know the individual default probabilities and we can calculate 𝐾_n,t = 𝛷^-1(p_n,t). Note that as (p_n,t) is a function of market spreads, we could in principle infer the default probabilities from the spreads in market data for similar types of borrowers. If we further assume that the default probabilities are equivalent for all obligors, we get the following expression for conditional default probability:

p(M_t)=φ((φ^-1(p_t)-sqrt(ρ_t)M_t)/sqrt(1-ρ_t))

Now, consider the fraction of losses on the portfolio at time t: FL_t. The unconditional distribution function of a portfolio characterized by a default probability p and correlation p is

F(FL*|p_t,ρ_t)=P(FL_t≤ FL*)

If we assume that the number of obligors tends to infinity, then due to the conditional independence assumption the fraction of losses FL_t converges to the individual default probability p(M_t). The unconditional distribution function of the fraction of losses can hence be expressed thus:

F(FL*|p_t,ρ_t)=P(FL_t≤ FL*)=

=P(p(M_t)≤ FL*)

=P[φ((φ^-1(p_t)-sqrt(ρ_t)M_t)/sqrt(1-ρ_t))≤ FL*]

=P[M_t≥ ((φ^-1(p_t-sqrt(1-ρ_t))φ^-1(FL*))/sqrt(ρ_t))]

=1-φ((φ^-1(p_t-sqrt(1-ρ_t))φ^-1(FL*))/sqrt(ρ_t))

=φ((sqrt(1-ρ_t)φ^-1(FL*)-φ^-1(p_t))/sqrt(ρ_t))

By changing the value of the fraction of losses 𝐹𝐿^∗for different steps and evaluating the cumulative probability, we can calculate the cumulative distribution function of the fraction of losses also called default rate. Deriving the latter distribution gives us the density of the default rate that can be used to calculate the loss distribution of the portfolio.

Empirical implementation

The density can also be calculated more directly by deriving the cumulative distribution over the fraction of losses. The above-mentioned relationship can then be expressed as the following density for the fraction of losses FL.

(ϕ (FL||p_t,ρ_t)=sqrt((1-ρ)/ρ)exp(&frac;1;2;&{;[φ^-1(FL²)]-[&frac;sqrt(1-ρ)φ^-1FL-φ^-1);p_t]²&};))

The density function can then be estimated by maximum likelihood. The maximum likelihood function is a function that depends on the probability of default and the coefficient of correlation where we will use the fraction of losses as an independent variable. The density (ϕ (FL||p_t,ρ_t) and the likelihood parameters are those that maximise the following product.

Likelihood*∏_t=1^T(ϕ (FL||p_t,ρ_t))

and it is typically transformed by applying so to maximize the log-likelihood function

Log-Likelihood*∑_t=1^Tln(ϕ (FL||p_t,ρ_t))

Which more explicitly gives

Log-Likelihood*∑_t=1^Tln(sqrt((1-ρ)/ρ))+&frac;1;2;&{;[φ^-1(FL²)-[&frac;sqrt(1-ρ)φ^-1FL-φ^-1);p_t]²&}

For standard credit portfolios, the time horizon is typically one year but for the fintech platform the credits are shorter so the method can be applied on shorter horizons such as one month or even less. The method then amounts to calculating the logarithm of the probability density of the fraction of losses for each observation on the fraction of losses. For the first step trial values for the probability of default and the coefficient of correlation are typically fixed. Basel guidelines for similar portfolios might be a good starting point. The solver or iteration can then estimate the values of the probability of default end the coefficient of correlation that maximise the log likelihood function which is the logarithm of the density for each observation. Those parameters can then be fed back into the formulas to determine the loss distribution.

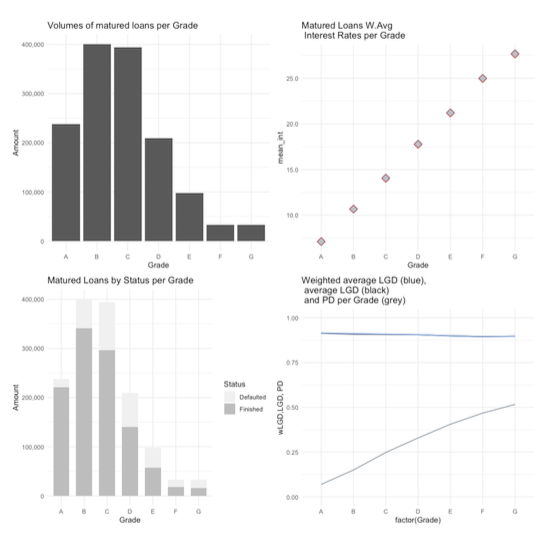
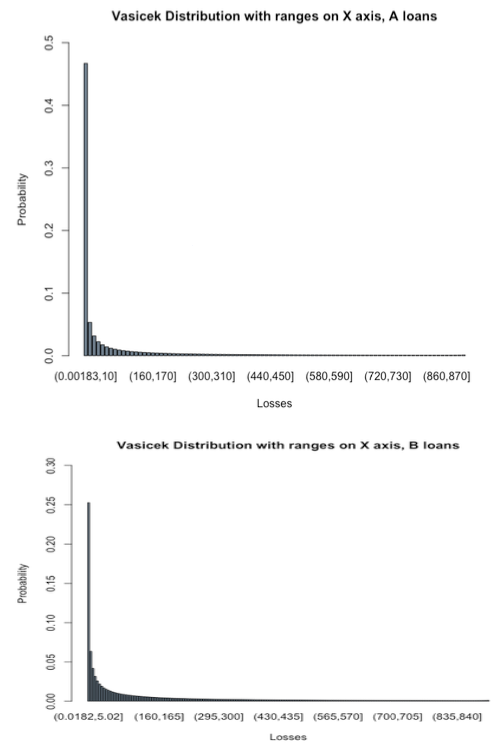
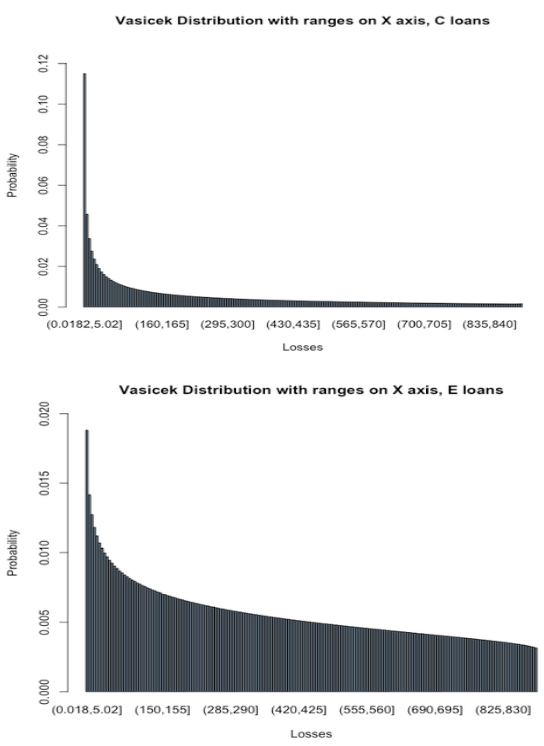
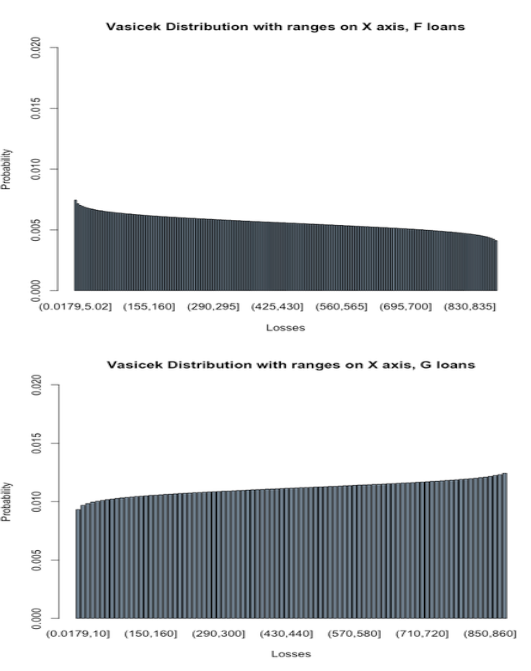
We implement the method with data from Lending Club using a Taylor-made R code. We first estimate the probability of default unconditionally from the loan datasets with different riskiness. We then use the maximum likelihood approach to estimate the parameter of correlation 𝜌. Those parameters are then put into the Vasicek formula which provides probabilities over fractions of losses. We can then simulate different levels of fractions of losses for the different loan portfolios of different risk categories from A (lowest risk) to G (highest risk). From the loss distributions, we can estimate the expected loss, the shortfall measure 𝑠_α(𝜔) for a given confidence interval 𝛼. The appendix presents the Figures with the properties of the Lending Club data as well as the estimated Vasicek distributions for each relevant loan category. We can now calculate the global target shortfall from investor risk profiles and determine the optimal portfolio weight using

μ(ω)-E(ω^TL|ω^TL≥ q_α(L^Tω))=∑_j=1ⁿω_j*[μ_j-E(L_j|ω^TL≥ q_α(L^Tω))]

which provides the weight of each subcomponent to reach the target shortfall as elicited from a potential decision maker. The table below indicates the estimated expected return and shortfall measures per risk bucket of Lending Club for a cutoff level α of 0.95. The weight1 column indicates the weights estimated using the above-mentioned equation.

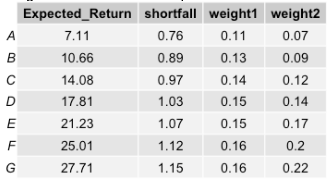
We also estimate the weights of the portfolio by evaluation the ratio of expected return over Expected shortfall. This is formally a risk adjusted performance measure (RAPM). By dividing each RAPM by the sum of RAPMs for all buckets we get the weight 2.

DISCUSSION AND CONCLUSIONS

This paper develops a portfolio and risk management approach for new emerging digital P2P platforms. We analyze the risk return profiles of different subunits of the P2P platform. We start by characterizing the risk measurement approach that is adapted to solve the coherent aggregation problem in a P2P platform. Then a portfolio approach based on shortfall measures is developed. Then the standard factor model approach with correlated Brownian motions enables us to characterize the loss distributions of the different portfolios. Using a Taylor-made R code we then estimate the different types of loss distributions from which we infer expected losses, expected shortfalls as well returns. This information can then be used in our portfolio optimization approach by any decision maker interested in risk management as well as investment. Further research will focus on implementation with different shortfall confidence intervals elicited from different risk profiles of decision makers.

APPENDIX

The appendix presents the collection of Figures evaluated from Lending Club data. We are grateful for research support and assistance from Alberts Vinklers and Emils Arcimovics from Sneakypeer for the coding in R.

REFERENCES

Acerbi, C. and Tasche, D. (2002) “On the coherence of expected shortfall”, Journal of Banking and Finance, Vol. 26, p. 1487-1503.

Artzner, P., Delbaen, F., Eber, J.-M. and Heath D. (1999) “Coherent Measures of Risk”, Mathematical Finance, Vol. 9, p. 203-228.

Balyuk, T. and Davydenko, S.A. (2018) “Reintermediation in Fintech: Evidence from online lending”, SSRN Working Paper.

Basak, S. and Shapiro, A. (2001) “Value at Risk based risk management: Optimal policies and asset prices”, Review of Financial Studies, p. 317-405.

Basel Committee on Banking Supervision (2020) “Sound management of risks related to money laundering and financing of terrorism”, Guidelines.

Begley, T. and Purnanandam, A. (2017) “Design of financial securities: Empirical evidence from private-label RMBS deals”, Review of Financial Studies 30, 120-161.

Bertsimas, D., Lauprete, G. and Samarov, A. “Shortfall as a risk measure: properties, optimization and applications”, Journal of Economic Dynamics and Control 28, 1353-1381.

Cambridge Center for Risk Studies (2016) “Managing Cyber Insurance Accumulation Risk” Claessens, St., Frost, J., Turner, G. and Zhu, F. (2018) “Fintech credit markets around the world: size, drivers and policy issues”, BIS Quaterly Review.

Committee on the Global Financial System and Financial Stability Board (2017) “FinTech credit: market structure, business models and financial stability implications”, CGFS papers May.

DeMarzo, P. and Duffie, D. “A liquidity-based model of security design”, Econometrica 67, 65-99. Denault, M. (2001) “Coherent allocation of Risk Capital”, Journal of Risk, 4(1), p. 1-34.

Dorfleitner, G. and Buch, A. (2008) “Coherent risk measures, coherent capital allocations and the gradient allocation principle”, Insurance:Mathematics and Economics, Vol. 42, p. 235-242. EIOPA (2018) “Understanding Cyber Insurance – A Structured Dialogue with Insurance Companies”, Publications office of the EU.

Fischer, T. (2003) “Risk Capital allocation by coherent risk measures based on one-sided moments”, Insurance: Mathematics and Economics, Vol. 32, P. 135-146.

Föllmer, H. and Schied, A. (2008) “Convex and Coherent Risk Measures”, Encyclopedia of Quantitative Finance, John Wiley and Sons.

Föllmer, H. and Schied, A. (2004) Stochastic Finance: An Introduction in Discrete Time, Gruyter Studies in Mathematices 27.

Fritzpatrick, T. and Mues, C. (2021) “How can lenders prosper? Comparing machine learning approaches to identify profitable peer-to-peer loan investments”, European Journal of Operational Research, 294(20, 711-722.

Garcia, R., Renault, E. and Tsafack, G. (2007) “Proper Conditioning for Coherent VaR in Portfolio Management”, Management Science, Vol. 53.

G-7 Cyber Expert Group (2017) Fundamental Elements for Effective Assessment of Cybersecurity in the Financial Sector, October. Washington DC: G-7

Guo, Y., Zhou, W., Luo, C., Liu, C. and Xiong, H. (2016) “Instance-based credit risk assessment for investment decisions in P2P lending”, European Journal of Operational Research, 249(2), 417-426.

Jiagtani, J. and Lemieux, C. (2017) “Fintech lending: Financial inclusion, risk pricing, and laternative information”, Technical Report, Federal Reserve Bank of Philadelphia

Kalkbrener, M. (2005) “An Axiomatic Approach to Capital Allocation”, Mathematical Finance, Vol. 15, p. 425-437.

Kim, A., Yang, Y., Lessman, S., Ma, T., Sung, M. and Johnson, J. (2019) “Can deep learning predict risky retail investors? A case study in financial risk behavior forecasting”, European Journal of Operational Research, 1-18.

Koijen, R. and Yogo, M. (2016) “Shadow Insurance”, Econometrica, Vol. 84, 1265-1287. Leland, H. and Pyle, D. (1977) “Informational asymmetries, financial structure and financial intermediation”, Journal of Finance 32, 371-387. Lewis, J. (2018) Economic Impact of Cybercrime—No Slowing Down. Santa Clara McAfee.

Liberti, J.M. and Petersen, M.A. (2019) “Information: Hard and Soft”, The Review of Corporate Finance Studies, 8(1), 1-41.

Miller, S. (2015) “Information and default in consumer credit markets: Evidence from a natural experiment”, Journal of Financial Intermediation 24(1), 45-70.

Milne, A. and Parboreeah, P. (2016) The business models and economics of Peer-to-Peer lending, Euro Credit Res Inst.

Omarini, E. (2018) “Peer-to-Peer Lending: Business Model Analysis and the Platform Dilemma”, International Journal of Finance, Economics and Trade. Serrano-Cinca, C. and Guttierez-Nieto, B. (2016) “The use of profit scoring as an alternative to credit scoring systems in pee-to-peer (P2P) lending”, Decision Support Systems 89, 113-122.

Stulz, R. (2019) “FinTech, BigTech and the future of Banks”, NBER Working Paper Series. US Department of the Treasury (2018) A financial system that creates economic opportunities: nonbank financials, fintech, and innovation, July.

Valleee, B. and Zheng, Y. (2019) “Marketplace lending: A new banking paradigm?”, The Review of Financial Studies, 32(5), 1939-1982.

Vasicek, O. (2002) “Loan Portfolio Value”, Risk, 15, December, 160-162.Verbraken, T., Bravo, C., Weber, R. and Baesens, B. (2014) “Development and application of consumer credit scoring models using profit-based classification measures”, 238(2), 505-513.